贝塞尔曲线
贝塞尔曲线(读作 [bezje])是一种使用数学方法描述的曲线,被广泛用于计算机图形学和动画中。在矢量图中,贝塞尔曲线用于定义可无限放大的光滑曲线。
贝塞尔曲线由至少两个控制点进行描述。Web 技术中使用的是三次贝塞尔曲线,即使用四个控制点 P0、P1、P2 和 P3 描述的曲线。
在绘制二次贝塞尔曲线的过程中,需要先作两条辅助线:P0 到 P1 和 P1 到 P2;第三条辅助线从其起点稳步移动到第一辅助线上,终点在第二辅助线上。在这条辅助线上,有一个点从其起点稳步移动到其终点。这个点描述的曲线就是贝塞尔曲线。以下是一个动画示例,展示了曲线的创建过程:
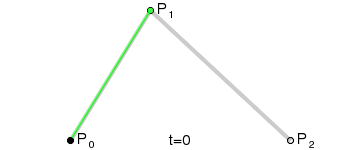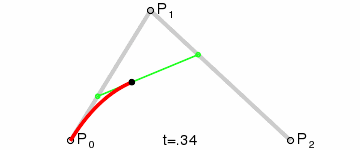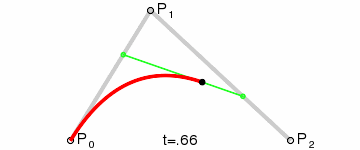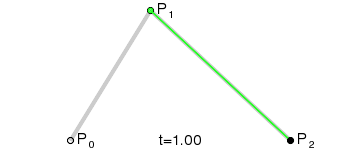
一般化
\(n\)阶贝塞尔曲线可如下推断。给定点\(P_0,P_1,P_2,\cdots,P_n\),其贝塞尔曲线即
\[ \displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}{n \choose i}\mathbf {P} _{i}(1-t)^{n-i}t^{i}={n \choose 0}\mathbf {P} _{0}(1-t)^{n}t^{0}+{n \choose 1}\mathbf {P} _{1}(1-t)^{n-1}t^{1}+\cdots +{n \choose n-1}\mathbf {P} _{n-1}(1-t)^{1}t^{n-1}+{n \choose n}\mathbf {P} _{n}(1-t)^{0}t^{n}{\mbox{ , }}t\in [0,1] \]
术语
一些关于参数曲线的术语,有
\[ {\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {P} _{i}\mathbf {b} _{i,n}(t),\quad t\in [0,1]} \]
\({\displaystyle \mathbf {b} _{i,n}(t)={n \choose i}t^{i}(1-t)^{n-i},\quad i=0,\ldots n}\)
又称作n阶的伯恩斯坦基底多项式,定义\(0^0\) = 1。
点\(P_i\)*称作贝塞尔曲线的控制点。多边形以带有线的贝兹点连接而成,起始于\(P_0\)并以\(P_n\)终止,称作贝兹多边形(或控制多边形)。贝兹多边形的凸包(convex hull)包含有贝塞尔曲线。
构建贝塞尔曲线
线性曲线
线性贝塞尔曲线函数中的t会经过由\(P_0\)至\(P_1\)的\(B(t)\)所描述的曲线。例如当t=0.25时,\(B(t)\)即一条由点至\(P_0\)至\(P_1\)路径的四分之一处。就像由0至1的连续t,描\(B(t)\)述一条由\(P_0\)至\(P_1\)的直线。
二次曲线
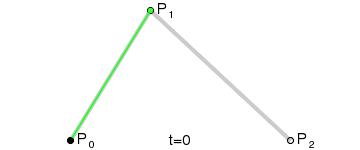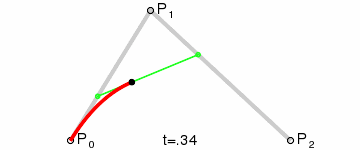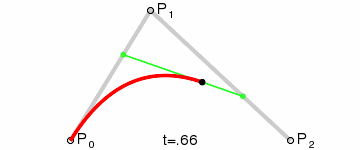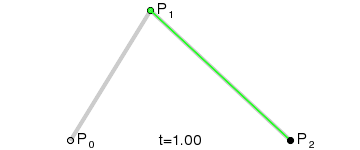
为建构二次贝塞尔曲线,可以中介点Q0和Q1作为由0至1的t:
- 由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
- 由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
- 由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。
高阶曲线
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1所建构:
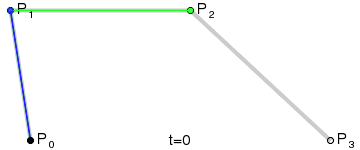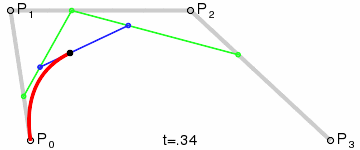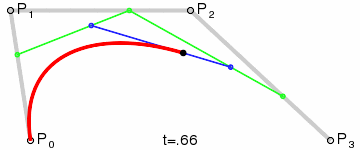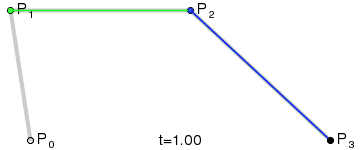
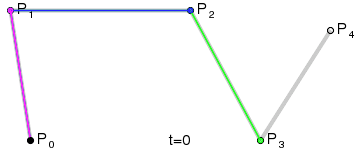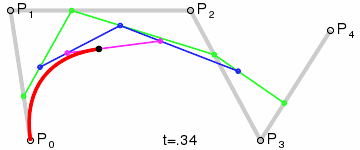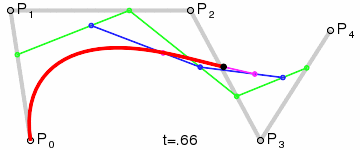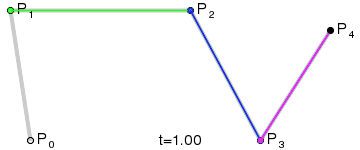
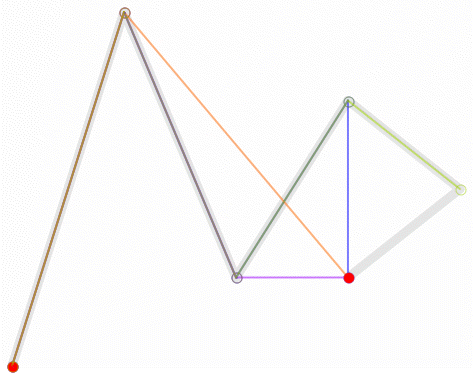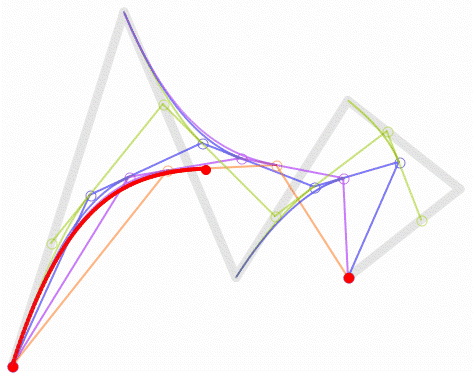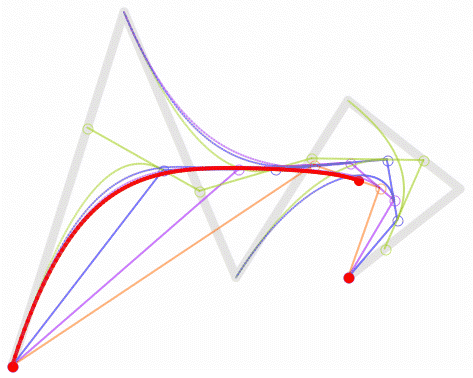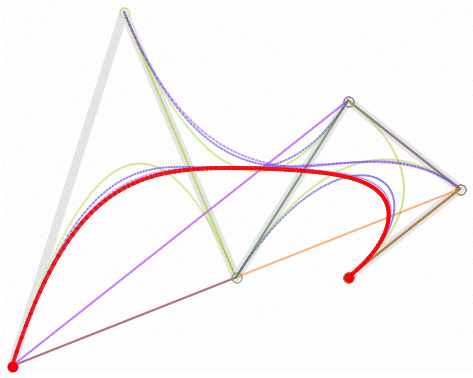
对于四次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2、Q3,由二次贝塞尔曲线描述的点R0、R1、R2,和由三次贝塞尔曲线描述的点S0、S1所建构:
升阶
n次贝塞尔曲线可以变换为一个形状完全相同的n+1次贝塞尔曲线。 这在软件只支持特定阶次的贝塞尔曲线时很有用。 例如,Cairo只支持三次贝塞尔曲线,你就可以用升阶的方法在Cairo画出二次贝塞尔曲线。
我们利用\({\displaystyle \mathbf {B} (t)=(1-t)\mathbf {B} (t)+t\mathbf {B} (t)}\)这个特性来做升阶。我们把曲线方程式中每一项\({\displaystyle \mathbf {b} _{i,n}(t)\mathbf {P} _{i}}\)都乘上 (1 − t) 或 t,让每一项都往上升一阶。以下是将二阶升为三阶的示例
\[ {\displaystyle {\begin{aligned}&{}\quad (1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+(1-t)^{2}t\mathbf {P} _{0}+2(1-t)^{2}t\mathbf {P} _{1}\\&{}\qquad +2(1-t)t^{2}\mathbf {P} _{1}+(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t{\frac {\mathbf {P} _{0}+2\mathbf {P} _{1}}{3}}+3(1-t)t^{2}{\frac {2\mathbf {P} _{1}+\mathbf {P} _{2}}{3}}+t^{3}\mathbf {P} _{2}\end{aligned}}} \]
对任何的n值,我们都可以使用以下等式
\[ {\displaystyle {n+1 \choose i}(1-t)\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i,n+1},\quad (1-t)\mathbf {b} _{i,n}={\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}} \] \[ {\displaystyle {n+1 \choose i+1}t\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i+1,n+1},\quad t\mathbf {b} _{i,n}={\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}} \] \[ {\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}+t\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}\\&=\sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}(t)\mathbf {P} _{i}+\sum _{i=0}^{n}{\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}(t)\mathbf {P} _{i}\\&=\sum _{i=0}^{n+1}\left({\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n+1}}\mathbf {P} _{i}\right)\mathbf {b} _{i,n+1}(t)=\sum _{i=0}^{n+1}\mathbf {b} _{i,n+1}(t)\mathbf {P'} _{i}\end{aligned}}} \]
式中\({\displaystyle \mathbf {P} _{-1}}\)和\({\displaystyle \mathbf {P} _{n+1}}\)可以任意挑选。
因此,新的控制点为 \[ {\displaystyle \mathbf {P'} _{i}={\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n+1}}\mathbf {P} _{i},\quad i=0,\ldots ,n+1.} \]