离散数学
复习章节：
第一章第7节的对偶不要求，第9节不要求，其他都要求
第二章第6节的前束合取/析取范式不要求，其他都要求
第三章第3节不要求，第8节warshall算法不要求，其他都要求
第四章第3节不要求，其他都要求
第五章第第6节不要求，第8节同余关系不要求，其他都要求
第七章全部要求
第一章 命题逻辑
1.1 命题及其表示法
真假可知但是不确定，认为是命题 
悖论
定义：命题 
1.2 联结词
1.3 命题公式与翻译
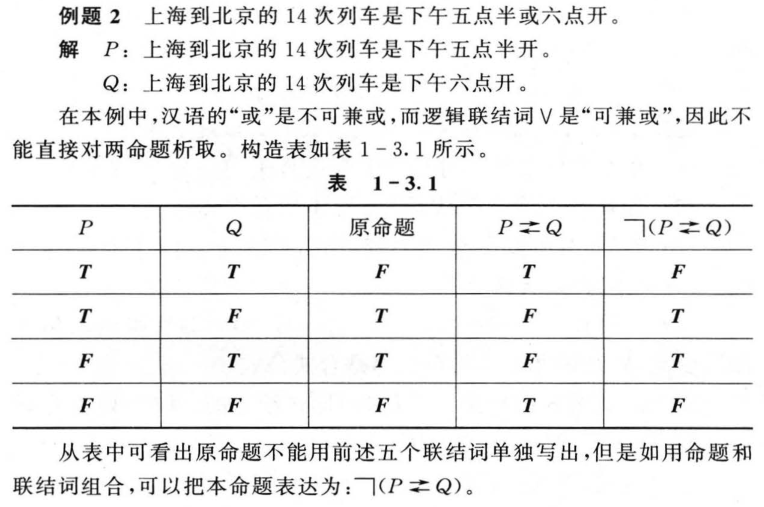
1.4 真值表与等价公式
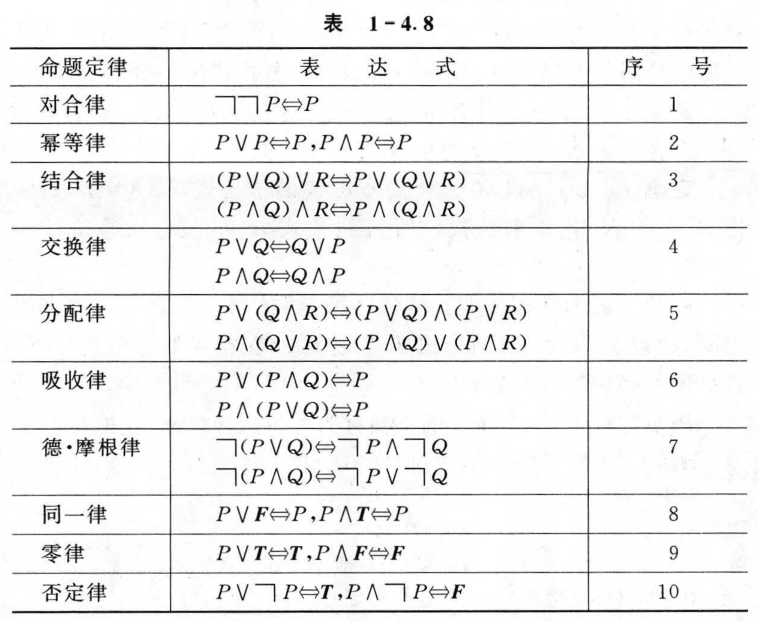
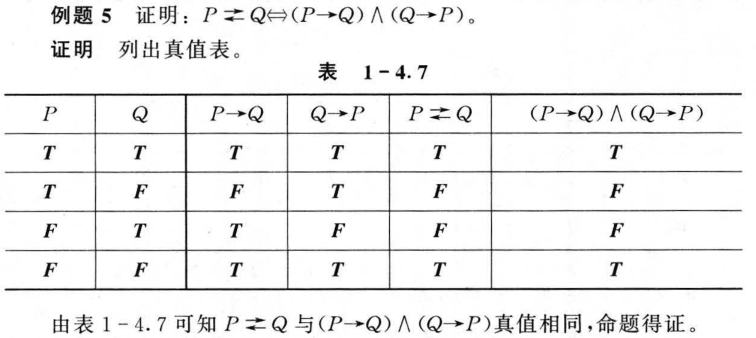
1.5 重言式与蕴含式
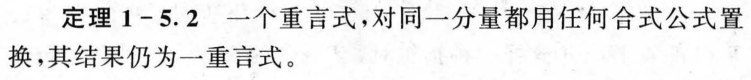
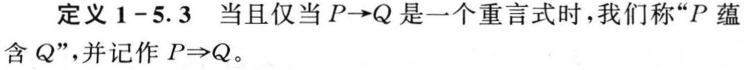
1.6 其他联结词
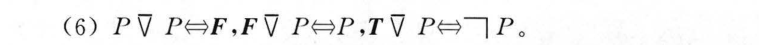
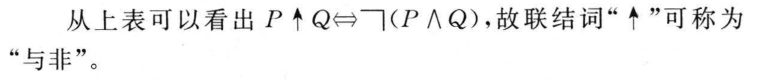
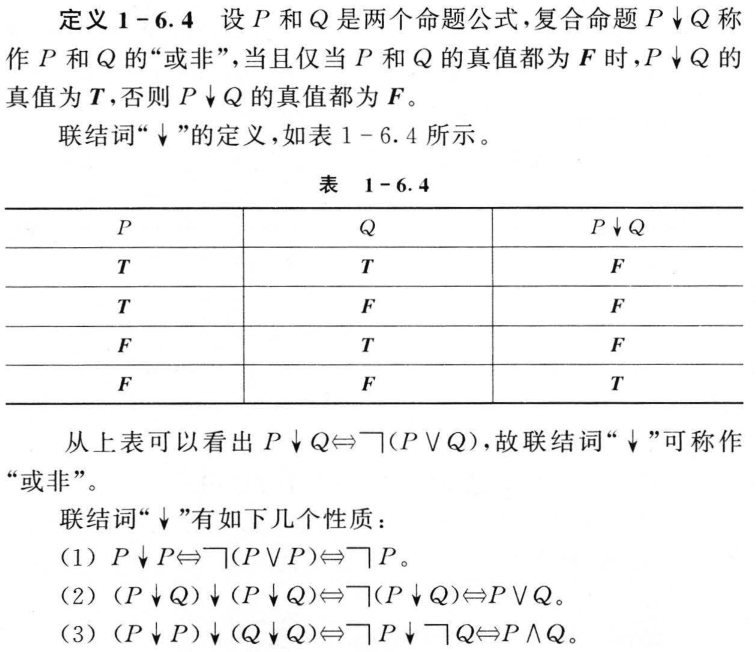
1.7 对偶与范式（对偶不要求）
1.8 推理理论
第二章 谓词逻辑
2.1 谓词的概念与表示
谓词定义：
2.2 命题函数与量词
2.3 谓词公式与翻译
2.4 变元的约束
2.5 谓词演算的等价式与蕴含式
2.6 前束范式
2.7 谓词演算的推理理论
第三章 集合论
3.1 集合的概念和表示法
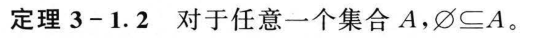
3.2 集合的运算
3.4 序偶与笛卡尔积
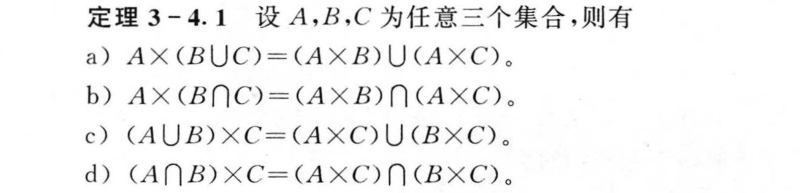
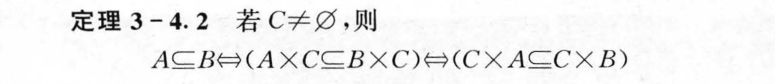
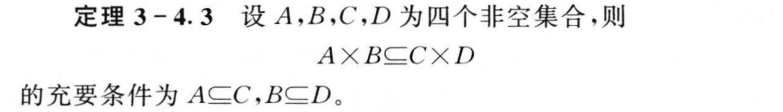
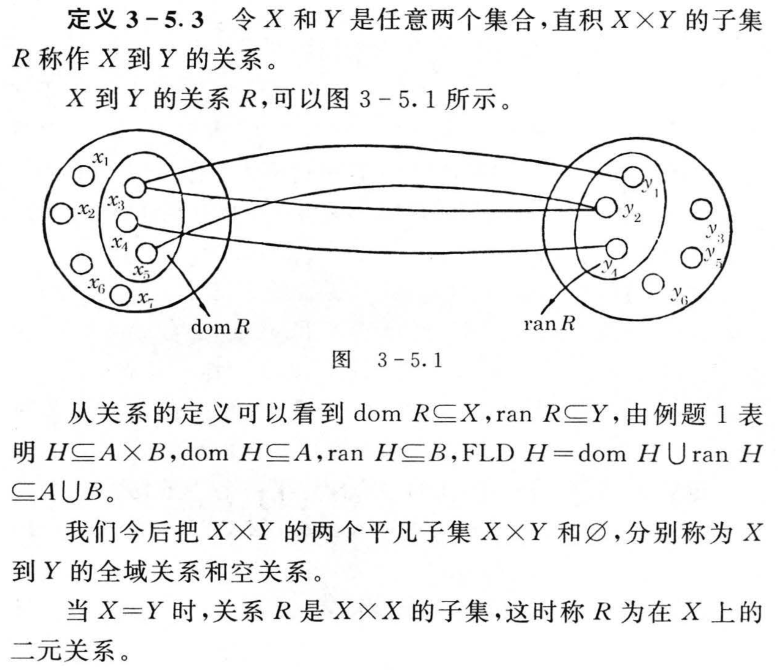
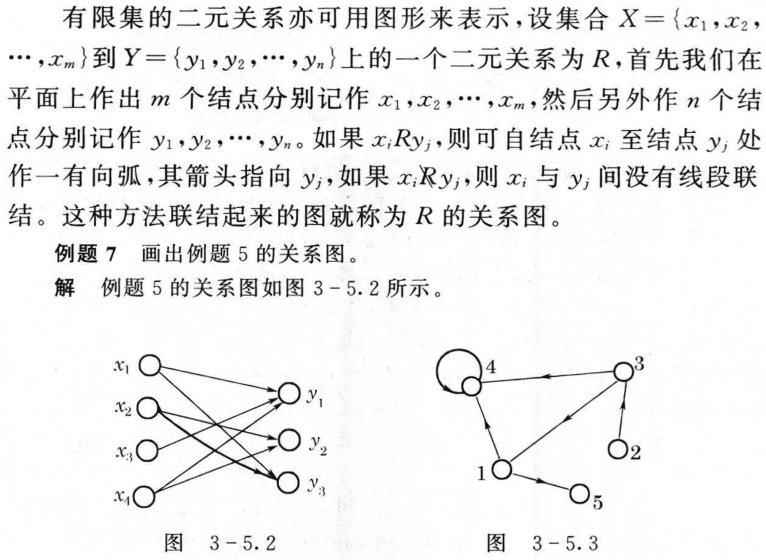
3.5 关系及其表示
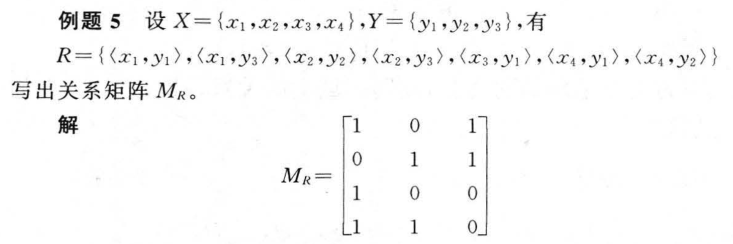
3.6 关系的性质
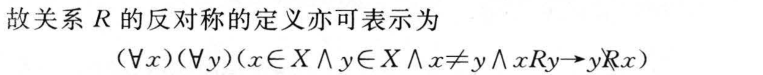
3.7 复合关系和逆关系
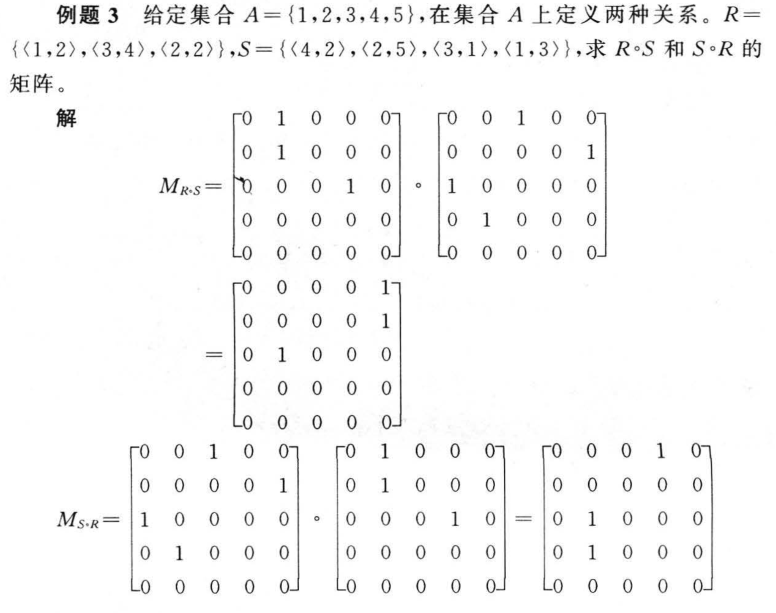
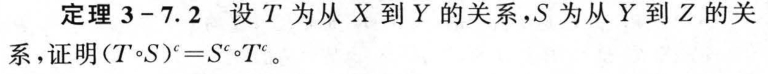
3.8 关系的闭包运算
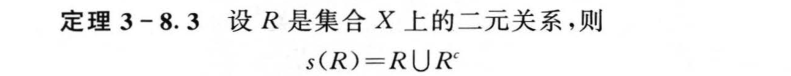
3.9 集合的划分和覆盖
3.10 等价关系与等价类
3.11 相容关系
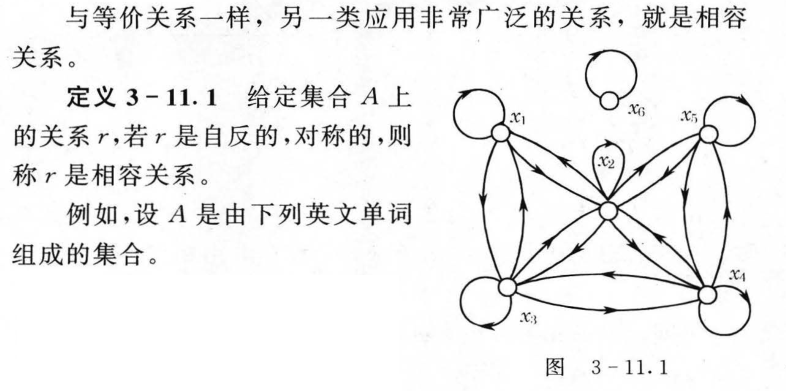
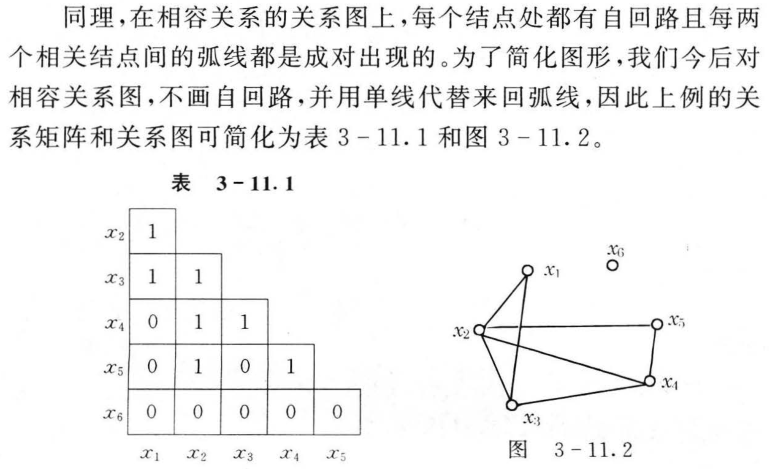
3.12 序关系（⭐）
第四章 函数
4.1 函数的概念
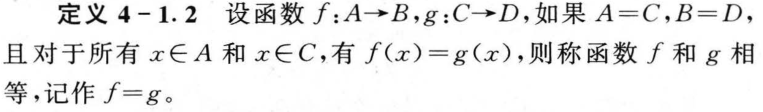
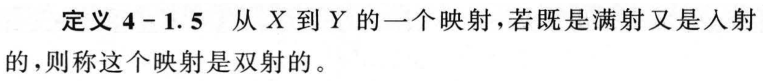
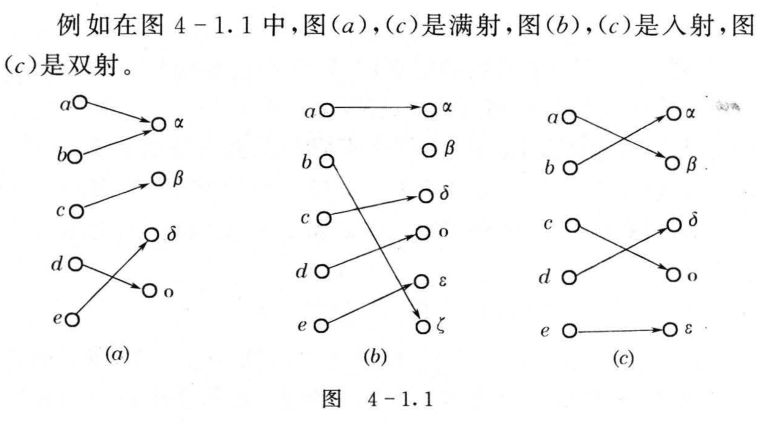
4.2 逆函数和复合函数
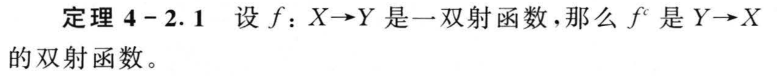
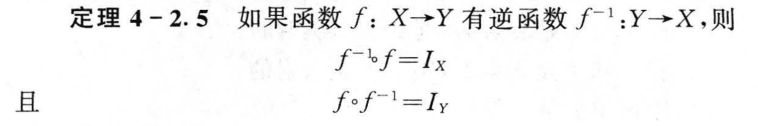
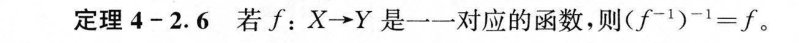
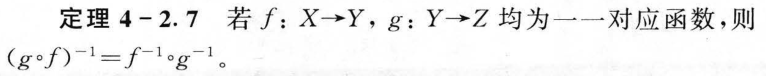
4.4 基数的概念
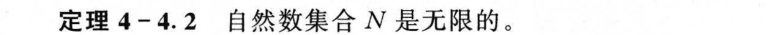
4.5 可数集与不可数集
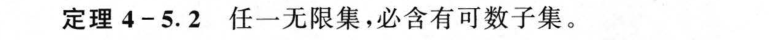
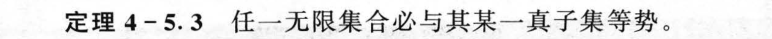
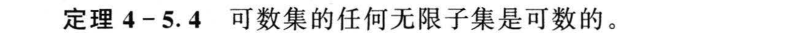
4.6 基数的比较
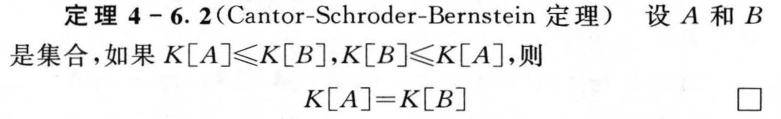
第五章 代数结构
5.1 代数系统的引入
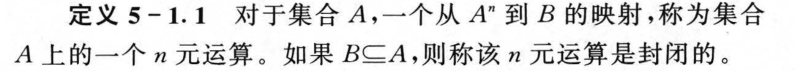
5.2 运算及其性质
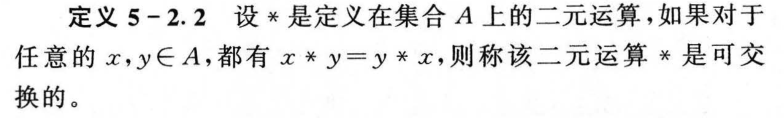
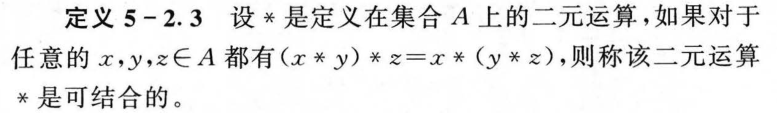
5.3 半群
5.4 群与子群
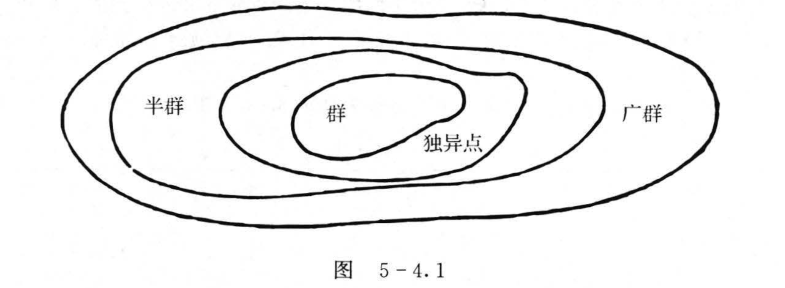
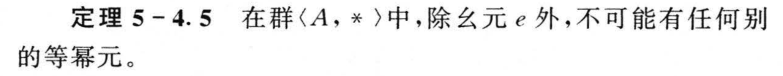
5.5 阿贝尔群与循环群
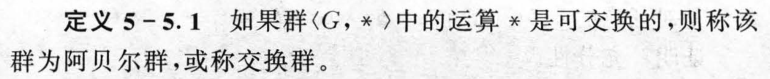
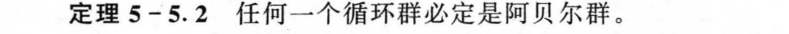
5.7 陪集与拉格朗日定理
5.8 同态与同构
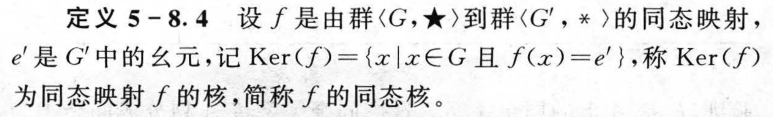
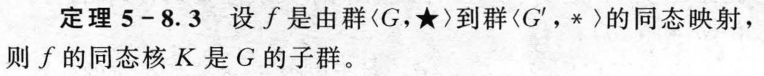
第七章 图论
7.1 图的基本概念
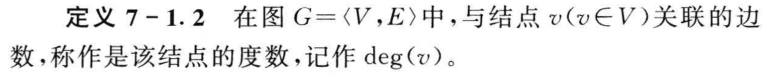
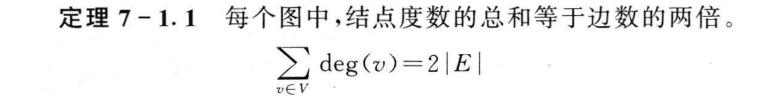
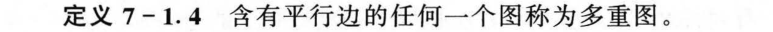
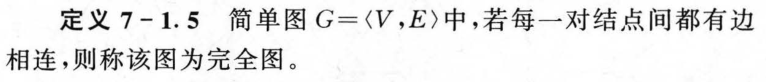
7.2 路与回路
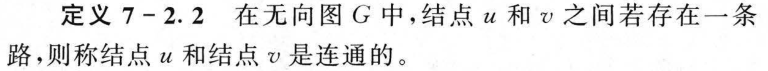
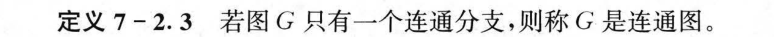
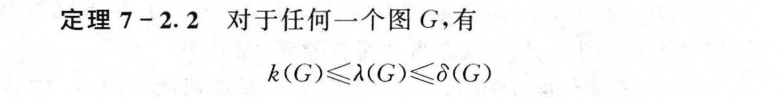
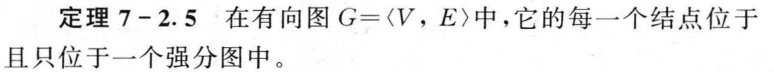
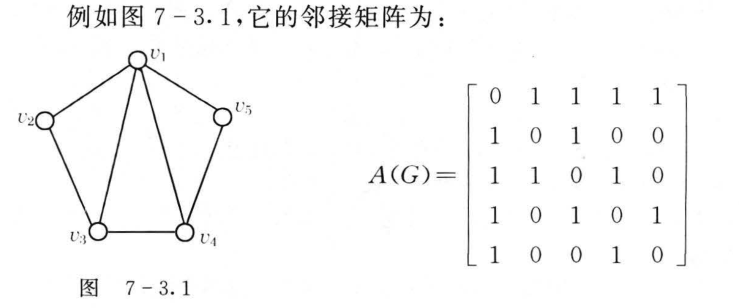
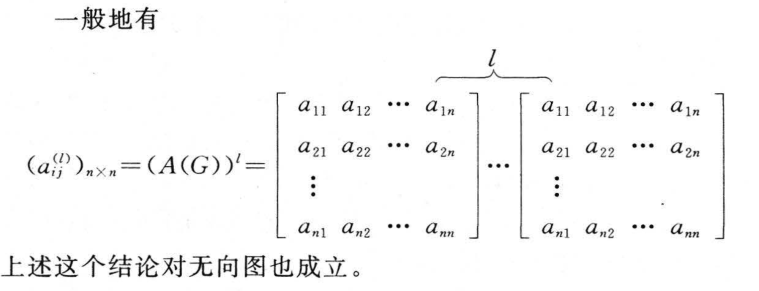
7.3 图的矩阵表示
7.4 欧拉图与汉密尔顿图
7.5 平面图
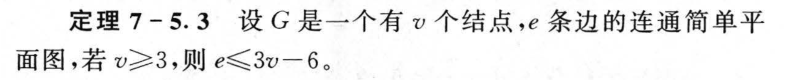
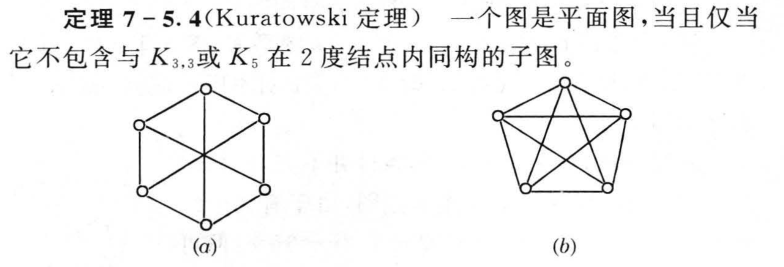
7.6 对偶图与着色
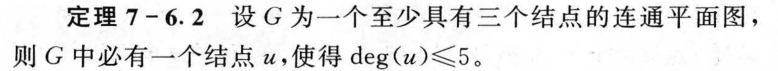
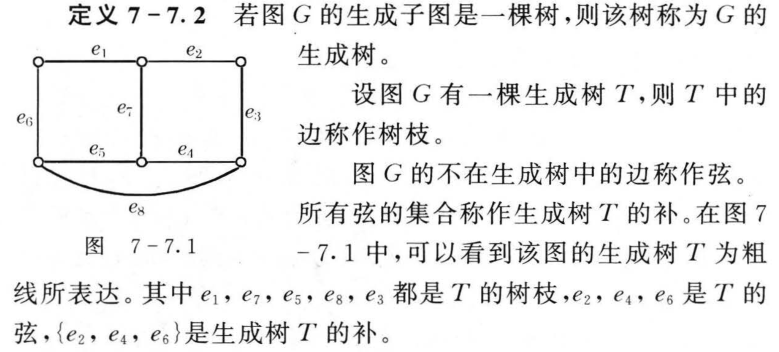
7.7 树与生成树
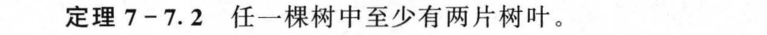
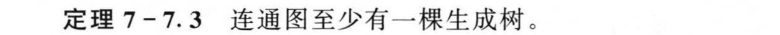
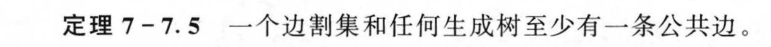
7.8 根树及其应用
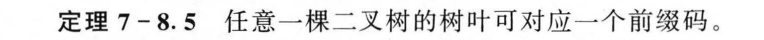
##重点习题
